Testing Jupyter Book features

Testing Jupyter Book features#

Warning

This is just a test page for trying things out and debugging the Jupyter book…

Note

The reason some features tested below do not work is because I am using JupyterBook 1, which does the rendering via Sphinx.

JupyterBook 2 uses a new MyST Document Engine and handles fancier Myst features that do not render properly here. See Upgrade for more information about the differences.

  • testing stirkethrough

Why don’t wiki: and doi: citations work like they should?#

You should also be able to hover over references as illustrated in the myst documentation

My _config.yml contains

myst_url_schemes: ["mailto", "http", "https", "wiki", "doi"]

but these don’t work…

using macros for websites?#

Latex#

Testing with some text from the Jupyter notebook for Chapter 7 of Riemann Problems and Jupyter Solutions [KLdR20].

Why don’t the equation references work properly in this? They do in other simple tests…

Chapter 7: Shallow Water Waves#

In this chapter we study a model for shallow water waves in one dimension:

(1)#\[\begin{align} h_t + (hu)_x & = 0, \label{SW_mass} \\ (hu)_t + \left(hu^2 + \frac{1}{2}gh^2\right)_x & = 0. \label{SW_mom} \end{align} \]

Here \(h\) is the depth, \(u\) is the velocity, and \(g\) is a constant representing the force of gravity. These equations are “depth averaged” and neglect vertical velocity and any vertical variations in the horizontal velocity. Viscosity and compressibility are neglected, and the pressure is assumed to be hydrostatic. Nevertheless, this is a surprisingly effective model for many applications, particularly when the wavelength is long compared to the fluid depth.

Hyperbolic structure#

We can write (\ref{SW_mass})-(\ref{SW_mom}) in the canonical form \(q_t + f(q)_x = 0\) if we define

(2)#\[\begin{align} q & = \begin{pmatrix} h \\ hu \end{pmatrix}, & f & = \begin{pmatrix} hu \\ hu^2 + \frac{1}{2}gh^2 \end{pmatrix}. \end{align} \]

In terms of the conserved quantities, the flux is

(3)#\[\begin{align} f(q) & = \begin{pmatrix} q_2 \\ q_2^2/q_1 + \frac{1}{2}g q_1^2 \end{pmatrix}. \end{align} \]

Thus the flux Jacobian is

(4)#\[\begin{align} f'(q) & = \begin{pmatrix} 0 & 1 \\ -(q_2/q_1)^2 + g q_1 & 2 q_2/q_1 \end{pmatrix} = \begin{pmatrix} 0 & 1 \\ -u^2 + g h & 2 u \end{pmatrix}. \end{align} \]

Its eigenvalues are

(5)#\[\begin{align} \label{SW:char-speeds} \lambda_1 & = u - \sqrt{gh}, & \lambda_2 & = u + \sqrt{gh}, \end{align} \]

with corresponding eigenvectors

(6)#\[\begin{align} \label{SW:fjac-evecs} r_1 & = \begin{bmatrix} 1 \\ u-\sqrt{gh} \end{bmatrix} & r_2 & = \begin{bmatrix} 1 \\ u+\sqrt{gh} \end{bmatrix} \end{align} \]

Notice that – unlike acoustics, but similar to the LWR traffic model – the eigenvalues and eigenvectors depend on \(q\). Because of this, the waves appearing in the Riemann problem move at different speeds and may be either jump discontinuities (shocks) or smoothly-varying rarefaction waves.

Equation (\ref{SW:char-speeds}).

The Riemann problem#

Consider the Riemann problem with left and right states

\[\begin{align*} q_\ell & = \begin{bmatrix} h_\ell \\ h_r u_\ell \end{bmatrix}, & q_r & = \begin{bmatrix} h_r \\ h_r u_r \end{bmatrix}. \end{align*}\]

Typically the Riemann solution consists of two waves, one related to each of the eigenvectors in (\ref{SW:fjac-evecs}). We refer to the wave related to \(r_1\) (the first characteristic family) as a 1-wave, and the wave related to \(r_2\) (the second characteristic family) as a 2-wave. Each wave may be a shock or rarefaction. There is a constant intermediate state \(q_m\) between them. In the figure below, we illustrate a typical situation in which the 1-wave happens to be a rarefaction and the 2-wave is a shock:

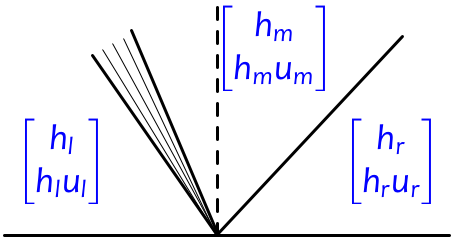
Structure of Riemann solution

In the figure we have one wave going in each direction, but since the wave speeds depend on \(q\) and can have either sign, it is possible to have both waves going left, or both going right. In these cases, the flow is said to be supercritical.

To solve the Riemann problem, we must find \(q_m\). To do so we must find a state that can be connected to \(q_\ell\) by a 1-shock or 1-rarefaction and to \(q_r\) by a 2-shock or 2-rarefaction. We must also ensure that the resulting waves satisfy the entropy condition.

Testing iframe#

Try embedding the shallow water Riemann solution interactive widget shown at the bottom of https://www.clawpack.org/riemann_book/

Contents